نرمالسازی دستهای اصطلاحی است که معمولاً در زمینه شبکههای عصبی کانولوشنی ذکر میشود. در این مقاله، قصد داریم بررسی کنیم که این مفهوم دقیقاً شامل چه مواردی است و چه تأثیری (در صورت وجود) بر عملکرد یا رفتار کلی شبکههای عصبی کانولوشنی دارد.
پیشنیازها
• پایتون: برای اجرای کدهای این مقاله، سیستم شما باید پایتون را نصب داشته باشد. خوانندگان باید تجربهی ابتدایی برنامهنویسی با پایتون را داشته باشند.
• مفاهیم پایه یادگیری عمیق: این مقاله مفاهیمی را پوشش میدهد که برای اعمال تئوری یادگیری عمیق ضروری هستند. از خوانندگان انتظار میرود که با اصطلاحات و مبانی اولیهی این حوزه آشنایی داشته باشند.
اصطلاح نرمالسازی
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as Datasets
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
import cv2
from tqdm.notebook import tqdm
import seaborn as sns
from torchvision.utils import make_grid
if torch.cuda.is_available():
device = torch.device(‘cuda:0’)
print(‘Running on the GPU’)
else:
device = torch.device(‘cpu’)
print(‘Running on the CPU’)
نرمالسازی در علم آمار به فرایند محدود کردن دادهها یا یک مجموعه از مقادیر در بازهی ۰ تا ۱ اشاره دارد. اما بهصورت ناخوشایندی، در برخی منابع، نرمالسازی همچنین به فرایند تنظیم میانگین یک توزیع داده روی صفر و انحراف معیار آن روی ۱ نیز اطلاق میشود.
در حقیقت، این فرایند که در آن میانگین توزیع روی ۰ تنظیم میشود و انحراف معیار آن برابر ۱ قرار میگیرد، استانداردسازی نام دارد. بااینحال، به دلیل برخی ملاحظات، به آن نرمالسازی یا نرمالسازی z-score نیز گفته میشود. مهم است که این تمایز را یاد بگیریم و به خاطر بسپاریم.
پیشپردازش دادهها
پیشپردازش داده به مراحلی اشاره دارد که قبل از ورودی داده به یک الگوریتم یادگیری ماشین یا یادگیری عمیق انجام میشوند. دو فرایند نرمالسازی و استانداردسازی که در بخش قبل ذکر شدند، از مراحل پیشپردازش داده محسوب میشوند.
نرمالسازی مین-ماکس (Min-max Normalization)
نرمالسازی مین-ماکس یکی از رایجترین روشهای نرمالسازی دادهها است. همانطور که از نامش پیداست، این روش نقاط داده را در بازهی ۰ تا ۱ محدود میکند. به این صورت که مقدار حداقل (min) در مجموعه داده به ۰ تنظیم میشود، مقدار حداکثر (max) به ۱ تبدیل میشود، و سایر مقادیر متناسب با این بازه مقیاسبندی میشوند.
فرمول زیر توصیف ریاضی این فرایند را ارائه میدهد. اساساً، این فرایند شامل کم کردن مقدار حداقل داده از هر نقطه داده و سپس تقسیم آن بر دامنهی (حداکثر – حداقل) است.

استفاده از تابع برای نرمالسازی مین-ماکس
با استفاده از تابع زیر، میتوانیم فرایند نرمالسازی مین-ماکس را شبیهسازی کنیم. این تابع به ما کمک میکند تا درک بهتری از آنچه در پشتصحنه اتفاق میافتد، داشته باشیم.
def min_max_normalize(data_points: np.array):
“””
این تابع دادهها را نرمالسازی کرده و آنها را در بازهی 0 تا 1 محدود میکند.
“””
# تبدیل لیست به آرایهی numpy (در صورت لزوم)
if type(data_points) == list:
data_points = np.array(data_points)
# ایجاد لیستی برای نگهداری دادههای نرمالشده
normalized = []
# محاسبهی حداقل و حداکثر مقدار در دادهها
minimum = data_points.min()
maximum = data_points.max()
# تبدیل آرایه به لیست برای پیمایش
data_points = list(data_points)
# نرمالسازی دادهها
for value in data_points:
normalize = (value – minimum) / (maximum – minimum)
normalized.append(round(normalize, 2))
return np.array(normalized)
ایجاد یک مجموعه تصادفی از مقادیر و اجرای نرمالسازی مین-ماکس
حال یک مجموعه از مقادیر تصادفی را با استفاده از NumPy ایجاد کرده و آنها را با تابع min_max_normalize که در بالا تعریف شد، نرمالسازی میکنیم.
# ایجاد مجموعهای از نقاط داده تصادفی
data = np.random.rand(50) * 20
# نرمالسازی دادهها
normalized = min_max_normalize(data)
مقایسهی توزیع دادهها قبل و بعد از نرمالسازی
در نمودارهای زیر میتوان مشاهده کرد که قبل از نرمالسازی، مقادیر در بازهی ۰ تا ۲۰ قرار داشتند و بیشتر دادهها بین ۵ تا ۱۰ بودند. اما بعد از نرمالسازی، مقدارها به بازهی ۰ تا ۱ محدود شدهاند و اکثریت دادهها بین ۰.۲۵ تا ۰.۵ قرار گرفتهاند.
نکته: هنگام اجرای این کد، توزیع دادهها ممکن است متفاوت باشد، زیرا مقادیر بهصورت تصادفی تولید میشوند.
# نمایش توزیع دادهها
figure, axes = plt.subplots(1, 2, sharey=True, dpi=100)
sns.histplot(data, ax=axes[0])
axes[0].set_title(‘بدون نرمالسازی’)
sns.histplot(normalized, ax=axes[1])
axes[1].set_title(‘نرمالشده با مین-ماکس’)

نرمالسازی Z-score
نرمالسازی Z-score، که همچنین استانداردسازی نامیده میشود، فرایند تنظیم میانگین و انحراف معیار یک توزیع داده به ترتیب برابر با 0 و 1 است. معادله زیر، معادله ریاضی است که نرمالسازی Z-score را تعیین میکند. این شامل کم کردن میانگین توزیع از مقدار موردنظر برای نرمالسازی قبل از تقسیم بر انحراف معیار توزیع است.

تابع تعریفشده در زیر، فرایند نرمالسازی Z-score را شبیهسازی میکند. با استفاده از این تابع، میتوانیم نگاهی دقیقتر به این فرایند داشته باشیم.
def z_score_normalize(data_points: np.array):
“””
این تابع دادهها را با محاسبه Z-score آنها نرمالسازی میکند.
“””
# تبدیل لیست به آرایهی NumPy
if type(data_points) == list:
data_points = np.array(data_points)
else:
pass
# ایجاد لیستی برای ذخیره دادههای نرمالشده
normalized = []
# محاسبه میانگین و انحراف معیار
mean = data_points.mean()
std = data_points.std()
# تبدیل به لیست برای انجام عملیات پیمایش
data_points = list(data_points)
# نرمالسازی دادهها
for value in data_points:
normalize = (value – mean) / std
normalized.append(round(normalize, 2))
return np.array(normalized)
با استفاده از توزیع دادهای که در بخش قبلی تولید شد، بیایید دادهها را با استفاده از تابع Z-score نرمالسازی کنیم.
# نرمالسازی دادهها
z_normalized = z_score_normalize(data)
# بررسی مقدار میانگین
z_normalized.mean()
>>>> -0.0006
# بررسی مقدار انحراف معیار
z_normalized.std()
>>>> 1.0000
دوباره، با استفاده از نمودارهای توزیع، میتوان مشاهده کرد که مقادیر توزیع اولیه در بازه 0 تا 20 قرار دارند، در حالی که مقادیر نرمالشده با Z-score اکنون حول 0 متمرکز شدهاند (میانگین صفر) و در بازهای تقریباً بین -1.5 تا 1.5 قرار گرفتهاند که یک بازهی قابل مدیریتتر است.
# مصورسازی توزیعها
figure, axes = plt.subplots(1, 2, sharey=True, dpi=100)
sns.histplot(data, ax=axes[0])
axes[0].set_title(‘unnormalized’)
sns.histplot(z_normalized, ax=axes[1])
axes[1].set_title(‘z-score normalized’)

دلایل پیشپردازش دادهها
در یادگیری ماشین، دادههای ورودی را بهعنوان ویژگیهای جداگانه در نظر میگیریم. معمولاً این ویژگیها در یک مقیاس یکسان قرار ندارند. بهعنوان مثال، یک خانه را در نظر بگیرید که دارای ۳ اتاق خواب و یک سالن نشیمن به مساحت ۴۰۰ فوت مربع است. این دو ویژگی در مقیاسهایی کاملاً متفاوت قرار دارند. حال اگر این دادهها را به یک الگوریتم یادگیری ماشین که توسط گرادیان نزولی بهینهسازی میشود وارد کنیم، فرآیند بهینهسازی دشوار خواهد شد؛ زیرا ویژگی با مقیاس بزرگتر تأثیر بیشتری نسبت به سایر ویژگیها خواهد داشت. بنابراین، برای سادهسازی فرآیند بهینهسازی، بهتر است همه ویژگیها را در یک مقیاس یکسان قرار دهیم.
نرمالسازی در لایههای کانولوشنی
در یک تصویر، دادههای ورودی همان مقادیر پیکسلی آن هستند. مقدار پیکسلها معمولاً بین ۰ تا ۲۵۵ متغیر است. به همین دلیل، قبل از وارد کردن تصاویر به یک شبکه عصبی کانولوشنی، بهتر است آنها را به گونهای نرمالسازی کنیم که تمام پیکسلها در یک بازه قابل کنترل قرار بگیرند.
حتی با انجام این کار، هنگام آموزش یک شبکه کانولوشنی، مقادیر وزنها (عناصر موجود در فیلترها) ممکن است بیشازحد بزرگ شوند و در نتیجه، نقشههای ویژگیای (Feature Maps) تولید کنند که مقادیر پیکسلی آنها در یک بازه وسیع پراکنده باشد. این امر باعث میشود که نرمالسازی انجامشده در مرحله پیشپردازش بیاثر شود. علاوه بر این، چنین وضعیتی میتواند فرآیند بهینهسازی را کند کرده یا در موارد شدید، منجر به مشکل «گرادیانهای ناپایدار» (Unstable Gradients) شود، که ممکن است مانع از بهینهسازی بیشتر وزنهای شبکه شود.
فرآیند نرمالسازی دستهای (Batch Normalization)
نرمالسازی دستهای (Batch Normalization) اساساً مقادیر پیکسلی تمام نقشههای ویژگی در یک لایه کانولوشنی را به یک میانگین و انحراف معیار جدید تنظیم میکند. بهطور معمول، این فرآیند با نرمالسازی Z-score همه پیکسلها آغاز میشود و سپس مقادیر نرمالشده در یک پارامتر دلخواه آلفا (مقیاس) ضرب شده و در نهایت، یک پارامتر دلخواه بتا (افست) به آن اضافه میشود.

این دو پارامتر، آلفا و بتا، پارامترهای قابل یادگیری هستند که شبکه عصبی کانولوشنی (ConvNet) از آنها برای اطمینان از قرار گرفتن مقادیر پیکسلها در نقشههای ویژگی در یک بازه قابل کنترل استفاده میکند. این کار، مشکل گرادیانهای ناپایدار را کاهش میدهد.
اجرای نرمالسازی دستهای (Batch Normalization in Action)
برای ارزیابی واقعی تأثیر نرمالسازی دستهای در لایههای کانولوشنی، باید دو شبکه عصبی کانولوشنی را مقایسه کنیم: یکی بدون نرمالسازی دستهای و دیگری با نرمالسازی دستهای. برای این منظور، از معماری LeNet-5 و مجموعه داده MNIST استفاده خواهیم کرد.
مجموعه داده و کلاس شبکه عصبی کانولوشنی
همانطور که قبلاً اشاره شد، در این مقاله از مجموعه داده MNIST برای انجام آزمایشها استفاده خواهد شد. این مجموعه داده شامل تصاویری با ابعاد ۲۸ × ۲۸ پیکسل از ارقام دستنویس است که مقادیر آنها از ۰ تا ۹ متغیر بوده و بهطور مناسب برچسبگذاری شدهاند.

این کد شامل دو بخش اصلی است:
۱. بارگیری مجموعه داده MNIST
۲. تعریف کلاس شبکه عصبی کانولوشنی (Convolutional Neural Network – CNN) و آموزش آن
۱. بارگیری مجموعه داده MNIST در PyTorch
مجموعه داده MNIST شامل تصاویر ۲۸×۲۸ پیکسلی از اعداد دستنویس ۰ تا ۹ است. اما برای استفاده از LeNet-5، تصاویر باید به ۳۲×۳۲ پیکسل تغییر اندازه داده شوند.
کد مربوط به بارگیری دادهها:
# بارگیری دادههای آموزشی
training_set = Datasets.MNIST(root=’./’, download=True,
transform=transforms.Compose([transforms.ToTensor(),
transforms.Resize((32, 32))]))
# بارگیری دادههای ارزیابی
validation_set = Datasets.MNIST(root=’./’, download=True, train=False,
transform=transforms.Compose([transforms.ToTensor(),
transforms.Resize((32, 32))]))
• مجموعه آموزشی ۶۰,۰۰۰ تصویر دارد.
• مجموعه اعتبارسنجی ۱۰,۰۰۰ تصویر دارد.
• تصاویر به تنسور (Tensor) تبدیل میشوند و به ۳۲×۳۲ تغییر اندازه داده میشوند.
۲. تعریف کلاس شبکه عصبی کانولوشنی (CNN)
در این بخش، کلاس ConvolutionalNeuralNet تعریف شده است که شامل متدهایی برای آموزش مدل، محاسبه دقت، و انجام پیشبینی است.
ویژگیهای کلاس:
• __init__(): مقداردهی اولیه مدل و تنظیم بهینهساز Adam.
• train(): شامل مراحل زیر است:
• مقداردهی اولیه وزنها با Xavier Initialization
• ایجاد DataLoader برای مجموعههای آموزشی و ارزیابی
• آموزش مدل با استفاده از تابع هزینه و بهروزرسانی وزنها
• محاسبه دقت مدل روی دادههای آموزشی و ارزیابی
• predict(): دریافت ورودی و خروجی شبکه را برمیگرداند.
کد مربوط به مقداردهی اولیه مدل:
class ConvolutionalNeuralNet():
def __init__(self, network):
self.network = network.to(device)
self.optimizer = torch.optim.Adam(self.network.parameters(), lr=1e-3)
• مدل روی GPU (اگر موجود باشد) یا CPU قرار میگیرد.
• بهینهساز Adam با نرخ یادگیری ۱e-3 تنظیم میشود.
۳. تابع آموزش (train())
این تابع شبکه عصبی را آموزش داده و دقت را محاسبه میکند.
مراحل:
1. ایجاد تابع مقداردهی اولیه وزنها:
def init_weights(module):
if isinstance(module, nn.Conv2d):
torch.nn.init.xavier_uniform_(module.weight)
module.bias.data.fill_(0.01)
elif isinstance(module, nn.Linear):
torch.nn.init.xavier_uniform_(module.weight)
module.bias.data.fill_(0.01)
• وزنهای لایههای Conv2D و Linear با Xavier Initialization مقداردهی میشوند.
2. ایجاد تابع محاسبه دقت مدل:
def accuracy(network, dataloader):
network.eval()
total_correct = 0
total_instances = 0
for images, labels in tqdm(dataloader):
images, labels = images.to(device), labels.to(device)
predictions = torch.argmax(network(images), dim=1)
correct_predictions = sum(predictions == labels).item()
total_correct += correct_predictions
total_instances += len(images)
return round(total_correct / total_instances, 3)
• مدل به حالت ارزیابی تغییر میکند.
• تعداد پیشبینیهای صحیح محاسبه و ذخیره میشود.
3. آموزش مدل برای epochs مشخص شده:
for epoch in range(epochs):
print(f’Epoch {epoch+1}/{epochs}’)
train_losses = []
# مرحله آموزش
print(‘training…’)
for images, labels in tqdm(train_loader):
images, labels = images.to(device), labels.to(device)
self.optimizer.zero_grad()
predictions = self.network(images)
loss = loss_function(predictions, labels)
loss.backward()
self.optimizer.step()
• مدل روی دادههای آموزشی اجرا میشود.
• تابع هزینه محاسبه و مقدار آن ذخیره میشود.
• گرادیان محاسبه و وزنها بهروزرسانی میشوند.
4. محاسبه دقت مدل روی دادههای ارزیابی:
with torch.no_grad():
print(‘deriving validation accuracy…’)
val_accuracy = accuracy(self.network, val_loader)
log_dict[‘validation_accuracy_per_epoch’].append(val_accuracy)
• مدل روی دادههای Validation تست میشود و دقت آن محاسبه میشود.
5. نمایش خروجی هر دوره (epoch):
print(f’training_loss: {round(train_losses, 4)} training_accuracy: ‘+
f'{train_accuracy} validation_loss: {round(val_losses, 4)} ‘+
f’validation_accuracy: {val_accuracy}\n’)
۴. پیشبینی با مدل (predict())
def predict(self, x):
return self.network(x)
• برای پیشبینی عدد دستنویس از مدل آموزشدیده شده استفاده میشود.
نتیجهگیری
این کد برای آموزش مدل LeNet-5 روی مجموعه داده MNIST طراحی شده است.
• از CNN برای تشخیص اعداد دستنویس استفاده میشود.
• دادهها به ۳۲×۳۲ تغییر اندازه داده شدهاند.
• از بهینهساز Adam برای بهروزرسانی وزنها استفاده شده است.
• مدل میتواند اعداد دستنویس جدید را پیشبینی کند.
LeNet-5

LeNet-5 (Y. Lecun et al) یکی از اولین شبکههای عصبی کانولوشنی است که بهطور خاص برای تشخیص و طبقهبندی تصاویر ارقام دستنویس طراحی شده است. معماری آن در تصویر بالا نمایش داده شده و پیادهسازی آن در PyTorch در کد زیر ارائه شده است.
class LeNet5(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.pool1 = nn.AvgPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.pool2 = nn.AvgPool2d(2)
self.linear1 = nn.Linear(5*5*16, 120)
self.linear2 = nn.Linear(120, 84)
self.linear3 = nn.Linear(84, 10)
def forward(self, x):
x = x.view(-1, 1, 32, 32)
#———-
# لایه ۱
#———-
output_1 = self.conv1(x)
output_1 = torch.tanh(output_1)
output_1 = self.pool1(output_1)
#———-
# لایه ۲
#———-
output_2 = self.conv2(output_1)
output_2 = torch.tanh(output_2)
output_2 = self.pool2(output_2)
#———-
# مسطحسازی
#———-
output_2 = output_2.view(-1, 5*5*16)
#———-
# لایه ۳
#———-
output_3 = self.linear1(output_2)
output_3 = torch.tanh(output_3)
#———-
# لایه ۴
#———-
output_4 = self.linear2(output_3)
output_4 = torch.tanh(output_4)
#————-
# لایه خروجی
#————-
output_5 = self.linear3(output_4)
return(F.softmax(output_5, dim=1))
با استفاده از معماری LeNet-5 تعریفشده در بالا، مدل model_1 را که عضوی از کلاس ConvolutionalNeuralNet است، با پارامترهای مشخصشده در کد زیر مقداردهی میکنیم. این مدل بهعنوان یک خط پایه برای اهداف ارزیابی استفاده خواهد شد.
# آموزش مدل ۱
model_1 = ConvolutionalNeuralNet(LeNet5())
log_dict_1 = model_1.train(nn.CrossEntropyLoss(), epochs=10, batch_size=64,
training_set=training_set, validation_set=validation_set)
پس از آموزش به مدت ۱۰ دوره و مشاهده دقتها از طریق لاگ متریکها، میبینیم که هر دو دقت آموزش و اعتبارسنجی در طول فرآیند آموزش افزایش یافتهاند. در این آزمایش، دقت اعتبارسنجی در ابتدا تقریباً ۹۳٪ در اولین دوره بود و سپس بهطور پیوسته طی ۹ تکرار بعدی افزایش یافت و در نهایت در دوره دهم به بیش از ۹۸٪ رسید.
sns.lineplot(y=log_dict_1[‘training_accuracy_per_epoch’], x=range(len(log_dict_1[‘training_accuracy_per_epoch’])), label=’training’)
sns.lineplot(y=log_dict_1[‘validation_accuracy_per_epoch’], x=range(len(log_dict_1[‘validation_accuracy_per_epoch’])), label=’validation’)
plt.xlabel(‘epoch’)
plt.ylabel(‘accuracy’)

LeNet-5 با نرمالسازی دستهای (Batch Normalized LeNet-5)

از آنجایی که موضوع این مقاله حول محور نرمالسازی دستهای در لایههای کانولوشنی است، نرمالسازی دستهای فقط در دو لایهی کانولوشنی موجود در این معماری اعمال شده است، همانطور که در تصویر بالا نشان داده شده است.
class LeNet5_BatchNorm(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.batchnorm1 = nn.BatchNorm2d(6)
self.pool1 = nn.AvgPool2d(2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.batchnorm2 = nn.BatchNorm2d(16)
self.pool2 = nn.AvgPool2d(2)
self.linear1 = nn.Linear(5*5*16, 120)
self.linear2 = nn.Linear(120, 84)
self.linear3 = nn.Linear(84, 10)
def forward(self, x):
x = x.view(-1, 1, 32, 32)
#———-
# LAYER 1
#———-
output_1 = self.conv1(x)
output_1 = torch.tanh(output_1)
output_1 = self.batchnorm1(output_1)
output_1 = self.pool1(output_1)
#———-
# LAYER 2
#———-
output_2 = self.conv2(output_1)
output_2 = torch.tanh(output_2)
output_2 = self.batchnorm2(output_2)
output_2 = self.pool2(output_2)
#———-
# FLATTEN
#———-
output_2 = output_2.view(-1, 5*5*16)
#———-
# LAYER 3
#———-
output_3 = self.linear1(output_2)
output_3 = torch.tanh(output_3)
#———-
# LAYER 4
#———-
output_4 = self.linear2(output_3)
output_4 = torch.tanh(output_4)
#————-
# OUTPUT LAYER
#————-
output_5 = self.linear3(output_4)
return F.softmax(output_5, dim=1)
آموزش مدل دارای Batch Normalization
با استفاده از قطعه کد زیر، مدل model_2 را که شامل نرمالسازی دستهای است مقداردهی اولیه میکنیم و آموزش آن را با همان پارامترهای model_1 آغاز میکنیم. سپس، امتیازات دقت را ارزیابی میکنیم.
# آموزش مدل ۲
model_2 = ConvolutionalNeuralNet(LeNet5_BatchNorm())
log_dict_2 = model_2.train(nn.CrossEntropyLoss(), epochs=10, batch_size=64,
training_set=training_set, validation_set=validation_set)
نتایج و تحلیل
با مشاهدهی نمودار، مشخص است که هر دو دقت آموزشی و اعتبارسنجی در طول آموزش مشابه مدل بدون نرمالسازی دستهای افزایش یافتهاند.
دقت اعتبارسنجی پس از اولین ایپاک بیش از 95٪ بود، یعنی ۳٪ بیشتر از model_1 در همان نقطه. سپس، این مقدار به تدریج افزایش یافت و در نهایت حدود 98.5٪ شد که 0.5٪ بالاتر از model_1 است.
sns.lineplot(y=log_dict_2[‘training_accuracy_per_epoch’],
x=range(len(log_dict_2[‘training_accuracy_per_epoch’])), label=’training’)
sns.lineplot(y=log_dict_2[‘validation_accuracy_per_epoch’],
x=range(len(log_dict_2[‘validation_accuracy_per_epoch’])), label=’validation’)
plt.xlabel(‘epoch’)
plt.ylabel(‘accuracy’)

مقایسه مدلها
با مقایسهی هر دو مدل، مشخص است که مدل LeNet-5 با لایههای کانولوشنی دارای نرمالسازی دستهای عملکرد بهتری نسبت به مدل معمولی بدون نرمالسازی دستهای داشته است. بنابراین، میتوان نتیجه گرفت که نرمالسازی دستهای در این مورد به بهبود عملکرد کمک کرده است.
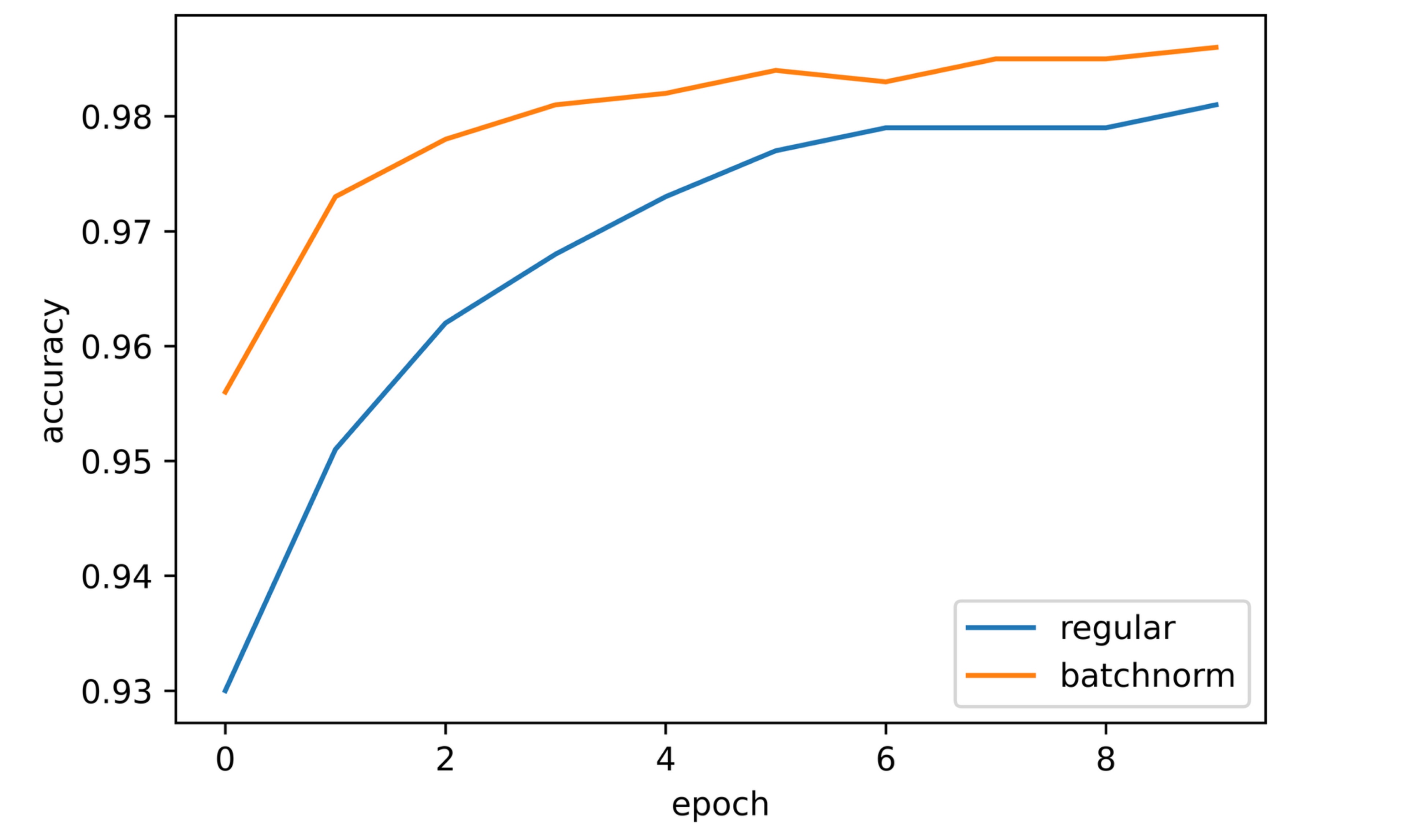
مقایسهی ضرایب خطا (Loss) در آموزش و اعتبارسنجی بین مدل LeNet-5 معمولی و مدل دارای نرمالسازی دستهای نشان میدهد که مدل دارای نرمالسازی دستهای سریعتر از مدل معمولی به مقادیر خطای پایینتر دست پیدا میکند. این موضوع نشاندهندهی این است که نرمالسازی دستهای سرعت بهینهسازی وزنهای مدل را در جهت صحیح افزایش میدهد، یا به عبارت دیگر، نرمالسازی دستهای سرعت یادگیری شبکهی کانولوشنی را افزایش میدهد.

ضرایب خطا در آموزش و اعتبارسنجی
نتیجهگیری نهایی
در این مقاله، مفهوم نرمالسازی را در زمینهی یادگیری ماشین و یادگیری عمیق بررسی کردیم. همچنین، فرآیندهای نرمالسازی را بهعنوان گامهایی در پیشپردازش دادهها مورد مطالعه قرار دادیم و دیدیم که چگونه نرمالسازی را میتوان فراتر از پیشپردازش دادهها و درون لایههای کانولوشنی از طریق نرمالسازی دستهای (Batch Normalization) بهکار گرفت.
سپس، فرآیند نرمالسازی دستهای را بررسی کرده و تأثیر آن را با مقایسهی دو نسخهی مختلف از مدل LeNet-5 (یکی بدون نرمالسازی دستهای و دیگری با نرمالسازی دستهای) بر روی مجموعه دادهی MNIST ارزیابی کردیم. نتایج نشان داد که نرمالسازی دستهای باعث افزایش عملکرد مدل و سرعت بهینهسازی وزنها میشود.
همچنین، برخی پیشنهاد کردهاند که نرمالسازی دستهای از تغییرات داخلی توزیع ویژگیها (Internal Covariate Shift) جلوگیری میکند، اما هنوز اجماع کاملی در این زمینه وجود ندارد.
Click to rate this post!
[Total: 0 Average: 0]





نظرات کاربران